螺栓聯(lián)接是工程結(jié)構(gòu)中應(yīng)用最廣泛的聯(lián)接形式之一,，具有結(jié)構(gòu)簡單,、裝拆方便和實(shí)用性強(qiáng)等特點(diǎn)。同時,，由于螺栓自身的聯(lián)接形式，它又成為了整個結(jié)構(gòu)中非線性因素的最主要來源,。

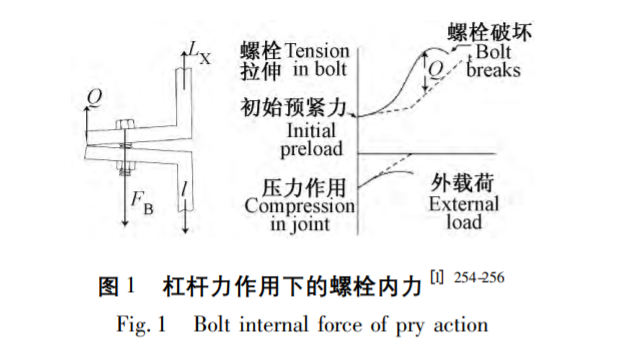
特別是當(dāng)其承受軸向拉伸杠桿力作用的時候,，即使制造螺栓的材料仍保持線性,，螺栓聯(lián)接的抗力也會呈現(xiàn)出非線性的“S型”,，如圖1所示[1]255。實(shí)際應(yīng)用中往往會將螺栓連接結(jié)構(gòu)簡化為線性系統(tǒng),，以達(dá)到方便,、快速的求解目的,。目前螺栓聯(lián)接剛度的計算中,，主 要關(guān)注的是安裝結(jié)構(gòu)不承受載荷作用的初始剛度，通常將承受軸向拉伸載荷作用的螺栓聯(lián)接結(jié)構(gòu)簡化成具有軸向剛度的彈簧[2]。

當(dāng)軸向杠桿力作用于螺栓聯(lián)接時，通常將結(jié)構(gòu)簡化為彈簧聯(lián)接剛性桿的1-D分析模型,，如圖2所示,。

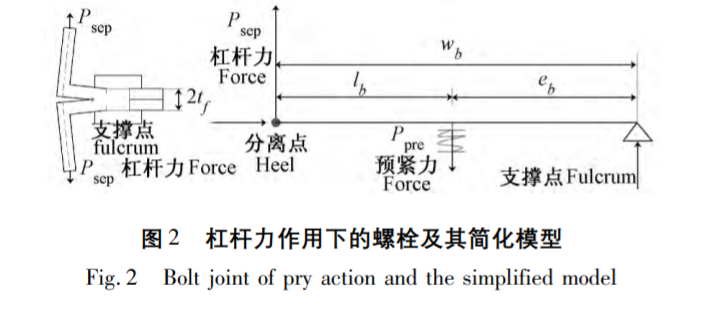
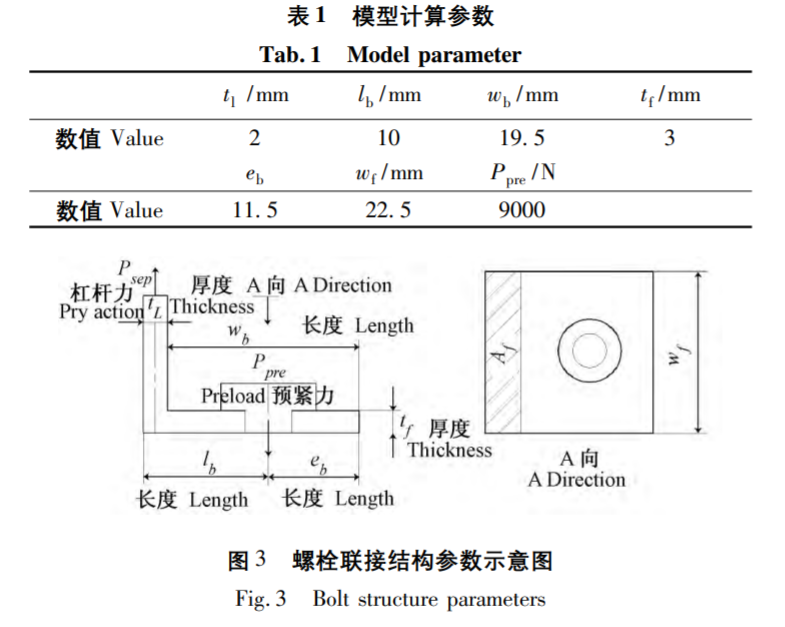
被聯(lián)接結(jié)構(gòu)假設(shè)為剛性，以“fulcrum”為支點(diǎn),，承受外部杠桿力Psep及螺栓預(yù)緊力Ppre的共同作用,，可以 將其簡化為如圖2，其中:

wb—杠桿力Psep與支撐點(diǎn)“fulcrum”之間的距離,；lb—杠桿力Psep與預(yù)緊力Ppre作用點(diǎn)之間的距離,；eb—預(yù)緊力Ppre作用點(diǎn)與支撐點(diǎn)“fulcrum”之間的距離。

根據(jù)力的平衡的關(guān)系,，可以得到如下：

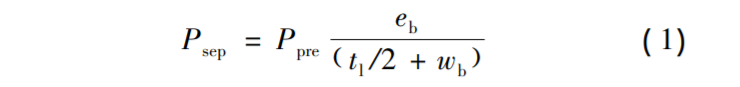
其中,，令fpry為杠桿力影響因子

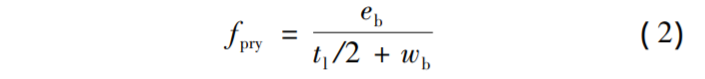
將式(2)簡化為

由式(3)不難發(fā)現(xiàn)，該假設(shè)條件下杠桿力的大小與預(yù)緊力和影響因子fpry成正比,。

①當(dāng)Ppre( 螺栓預(yù)緊力)一定的條件下,，外載荷作用線與螺栓預(yù)緊力作用點(diǎn)之間距離lb越近，該結(jié)構(gòu)所能承受的外力就越大,，螺栓聯(lián)接所表現(xiàn)出的整體剛度就越大,。

②當(dāng)螺栓聯(lián)接結(jié)構(gòu)確定(即fpry參數(shù)一定)的條件下，預(yù)緊力越大,，結(jié)構(gòu)能夠承受的杠桿力就越大,。

真實(shí)的螺栓結(jié)構(gòu)在服役過程中，如壓力容器,，航空發(fā)動機(jī)機(jī)匣等采用螺栓法蘭進(jìn)行聯(lián)接的結(jié)構(gòu)[3]1-3[4-5],；車輛底架吊裝的制動裝置，高速動車組設(shè)備艙裙板等[6],。預(yù)緊力,、螺孔位置都會對其軸向聯(lián)接杠桿力產(chǎn)生較顯著的影響,，且這些影響中均包含了非線性性質(zhì)。明確這些影響因素的作用規(guī)律,，對于設(shè)計合理的承受軸向拉伸載荷的螺栓聯(lián)接往往是至關(guān)重要的,，而采用簡單的 1-D 模型顯然無法滿足這一需求。

本文建立了螺栓聯(lián)接結(jié)構(gòu)的精細(xì)的有限元模型,， 采用Abaqus對其進(jìn)行了數(shù)值仿真分析,，分析中充分考慮了結(jié)構(gòu)的材料非線性和接觸非線性，同時根據(jù)上述簡化模型的結(jié)果,，選取螺栓聯(lián)接的設(shè)計過程中預(yù)緊力和預(yù)緊力作用位置兩個主要因素,，明確其影響規(guī)律，對上述參數(shù)對結(jié)構(gòu)聯(lián)接剛度變化的影響進(jìn)行分析,，提出杠桿力作用下螺栓聯(lián)接剛度變化的計算模型,。

1 杠桿力作用下的螺栓聯(lián)接模型

1 模型基本參數(shù)

本文以M6螺栓聯(lián)接結(jié)構(gòu)為研究對象,，選取一個如圖3所示的基本參數(shù)的結(jié)構(gòu)模型,，各參數(shù)的數(shù)值如表1所列。

2 有限元模型基本參數(shù)

1. 2. 1 單元類型選擇

本文利用Abaqus建立螺栓聯(lián)接精細(xì)有限元分析模型,，為了更好的選擇單元類型,，作者首先采用不同單元進(jìn)行了試算，并得出以下兩點(diǎn)結(jié)論:

( 1) 默認(rèn)的減縮積分單元在高應(yīng)變區(qū)會產(chǎn)生非物理性位移的“沙漏現(xiàn)象”,，因此采用完全積分單元進(jìn)行計算,。

( 2) 二階六面體單元的與一階六面體單元計算結(jié)果沒有明顯的區(qū)別，均可以滿足數(shù)值仿真的精度,。

綜合考慮上述分析,，并盡量節(jié)省計算所需的時間， 本文建議采用一階六面體單元C3D8 進(jìn)行模型網(wǎng)格劃分,，螺栓與被聯(lián)接結(jié)構(gòu)以及聯(lián)接結(jié)構(gòu)之間的幾何非線性則采用“硬接觸”摩擦進(jìn)行模擬,。

2. 2 網(wǎng)格密度的選擇

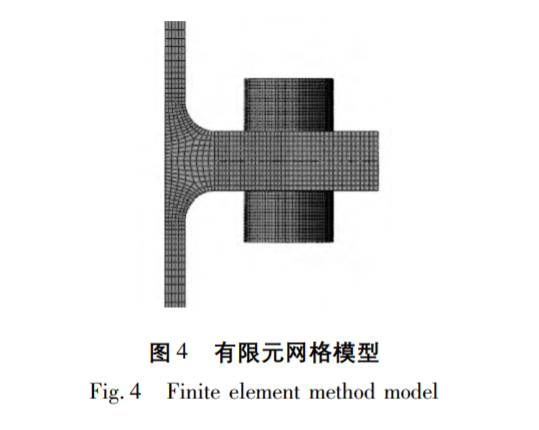
2010 年，Grant M. Henson[3]9-11在針對如圖3所示的聯(lián)接結(jié)構(gòu)模型建立時,，討論了相關(guān)網(wǎng)格大小的參數(shù),， 本文根據(jù)其論文計算結(jié)論分別采用1mm～3mm單元長度并進(jìn)行了驗(yàn)證，計算結(jié)果誤差在5%以內(nèi),，因此選擇較為經(jīng)濟(jì)的分析模型即單元長度為3mm進(jìn)行模型建立,，共劃分了16071個結(jié)點(diǎn)，12614個單元,，如圖 4 所示,。

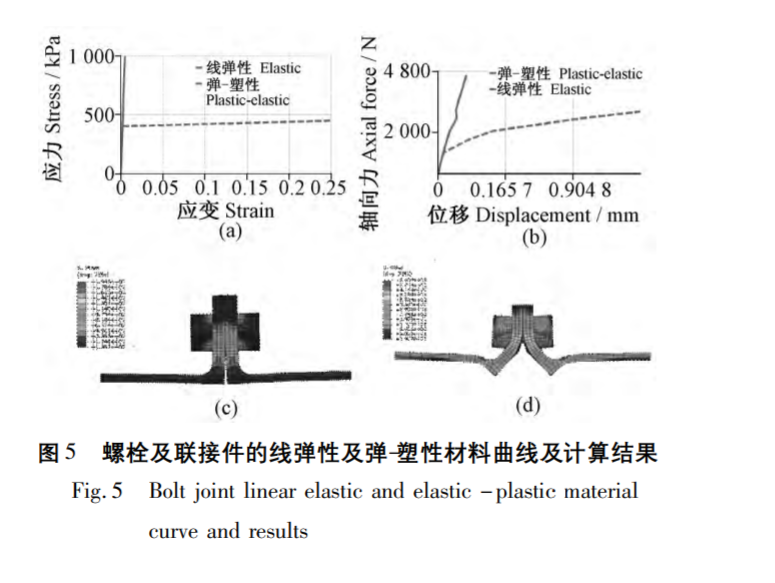
相同邊界條件杠桿力外載荷Psep加載范圍0N～4600N，對圖3所示的模型采用圖4網(wǎng)格,，在相同邊界條件下分別采用彈性及彈-塑性材料對模型進(jìn)行簡單的校驗(yàn)分析,，材料參數(shù)曲線如圖5a所示,，計算結(jié)果如圖5c和5d所示，相同作用力下的軸向力和軸向位移之間的關(guān)系如圖5b所示,。

從計算結(jié)果中可以看出螺栓在承受杠桿力作用過程中,，聯(lián)接結(jié)構(gòu)在螺栓預(yù)緊力作用下會出現(xiàn)局部的屈服現(xiàn)象，這會在很大程度上影響結(jié)構(gòu)的整體性能,，為了更確切的描述結(jié)構(gòu)的服役狀態(tài),，分析中引入了材料的塑性以得到更為合理的數(shù)值仿真結(jié)果。

對于本文計算螺栓整體聯(lián)接剛度的分析,，首先需要確定螺栓聯(lián)接外載荷作用的范圍,，利用強(qiáng)度極限與螺栓的有效面積估算螺栓保證剛度的極限拉伸值，M6 螺栓聯(lián)接的計算結(jié)果為1500N,，按照該數(shù)值進(jìn)行加載,，可以確定采用彈性材料及彈塑性材料結(jié)果基本一致[7]。

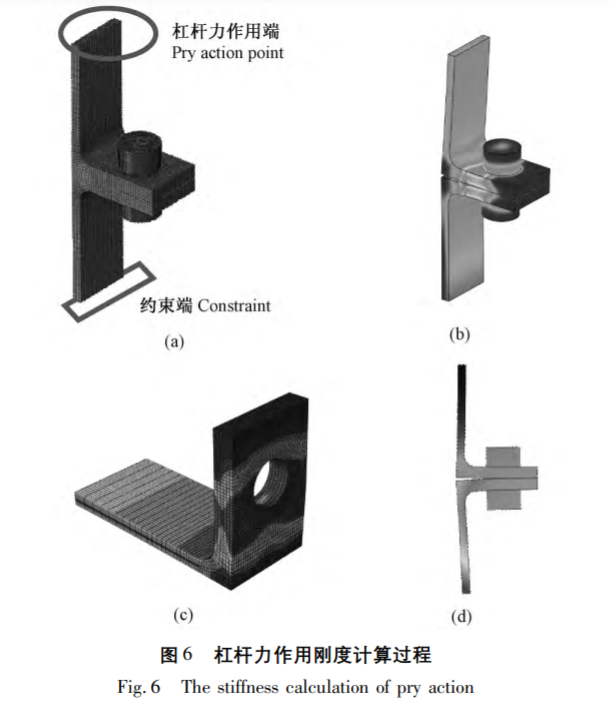
2 杠桿力作用下的影響參數(shù)分析：2. 1預(yù)緊力Ppre的影響分析根據(jù)剛度的基本定義結(jié)構(gòu)能夠抵抗變形的能力,， 首先將模型一端固定,，施加螺栓預(yù)緊力，預(yù)緊力Ppre變化范圍是 6000N～12000N,，完成螺栓預(yù)緊力施加后,，進(jìn)行另一端的杠桿力加載，如圖6a所示,，計算過程中定義外載荷加載步長為60N,，根據(jù)上述分析得出0N～1500N杠桿力作用的計算結(jié)果，如圖6b所示,，由于定義了接觸面間的接觸關(guān)系,，計算結(jié)果提取軸向接觸力的大小變化作為計算外載荷Fz，如圖6c所示,，軸向變形由接觸面間隙取最大點(diǎn)的平均位移差如圖6d所示[8],。

杠桿力變化過程中螺栓聯(lián)接結(jié)構(gòu)的剛度Kpry，如式( 4) 所示：

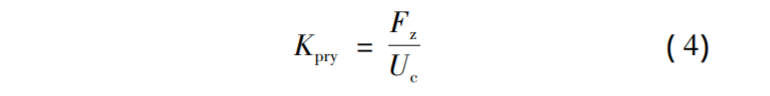
Fz—杠桿力作用下的接觸面軸向力;

Uc—軸向分離聯(lián)接結(jié)構(gòu)的位移;

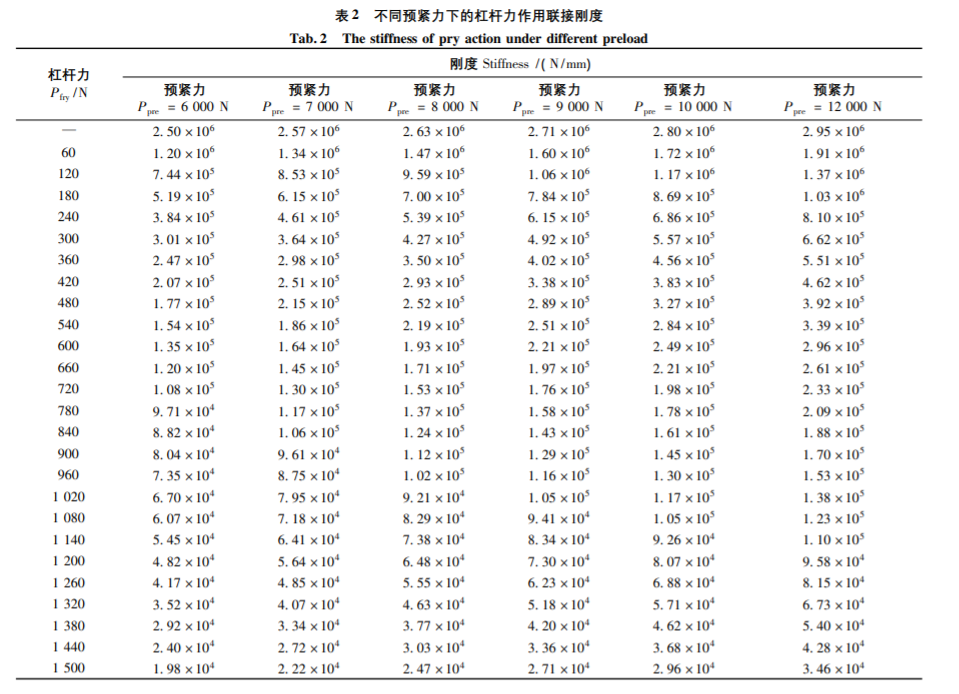
根據(jù)螺栓M6計算的杠桿力極限進(jìn)行加載,，討論該載荷作用下的螺栓聯(lián)接剛度變化,，計算結(jié)果如表2所列。

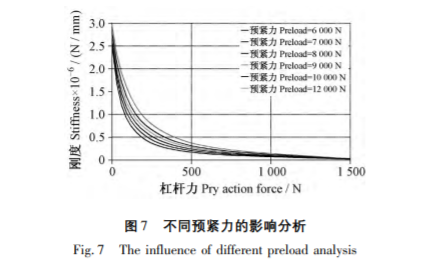
根據(jù)杠桿力作用的變化,，利用Abaqus求解螺栓聯(lián)接剛度的數(shù)據(jù)列于表2中,，結(jié)果變化如圖7所示，分析不難得到以下規(guī)律：

(1) 聯(lián)接初始剛度隨著預(yù)緊力的增加而增加,， 預(yù)緊力增加100%的條件下,，初始剛度增加 13% ，作為聯(lián)接結(jié)構(gòu)中一個重要的影響因素預(yù)緊力可以提高螺栓聯(lián)接的初始剛度,，但是上述分析結(jié)果表明該因素的影響較為有限,，實(shí)際過程中只要能保證一定的預(yù)緊力就可以保證有效的初始剛度,，而過大的預(yù)緊力如若控制不當(dāng)或者偶然過載，反而會導(dǎo)致連接的失效,。

( 2) 相同預(yù)緊力條件下隨著杠桿力的增加,，螺栓聯(lián)接剛度迅速下降，下降比例超過50% ,，該計算結(jié)果與文獻(xiàn)[3]23- 26結(jié)果相吻合,。杠桿力作用下的不同預(yù)緊力的聯(lián)接整體剛度隨杠桿力變化如圖7所示，隨著杠桿力的增加,，初始狀態(tài)的聯(lián)接剛度迅速下降,，當(dāng)杠桿力達(dá)到M6螺栓彈性極限值時，預(yù)緊力對剛度的影響基本趨于一致,。

綜合上述分析,，預(yù)緊力作為聯(lián)接的最重要因素，其對聯(lián)接剛度的影響并不是非常大,，保證有效的預(yù)緊力即可以達(dá)到滿意的聯(lián)接初始剛度,。而對于包含有螺栓聯(lián)接結(jié)構(gòu)的模型進(jìn)行動力學(xué)分析，不僅僅是其結(jié)合面阻尼的耗散占結(jié)構(gòu)總耗散的90%以上[9],，其結(jié)構(gòu)剛度的變化同樣對動力學(xué)特性有很大的影響,。

2. 2 杠桿力因子

fpry的影響分析公式(4) 中可以得出對杠桿力最直接的影響因素除了上述的預(yù)緊力還有外載荷作用線與螺栓軸線之間距離lb,，該距離越短,，相同條件下螺栓結(jié)構(gòu)能承受的杠桿力就越大。在預(yù)緊力給定的條件下本節(jié)中調(diào)整上述模型中的lb長度,，確定其在總長中的比例,， 建立8個模型，在相同杠桿力作用下對該參數(shù)進(jìn)行討論分析,。

將上述8個模型杠桿力作用的聯(lián)接剛度變化列于表5中,，同時對不同模型在杠桿力作用下的軸向力-軸向位移分析數(shù)據(jù)，結(jié)果變化如圖8所示,，不難得到下面的結(jié)論:

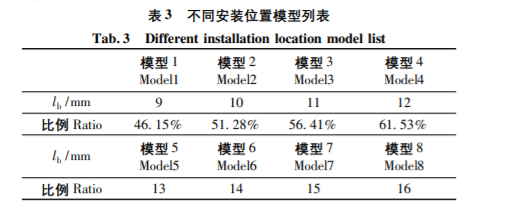
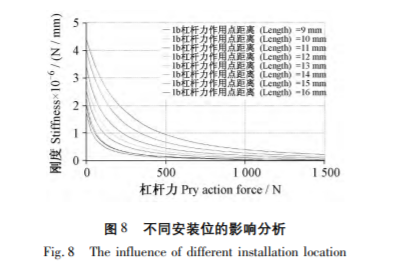
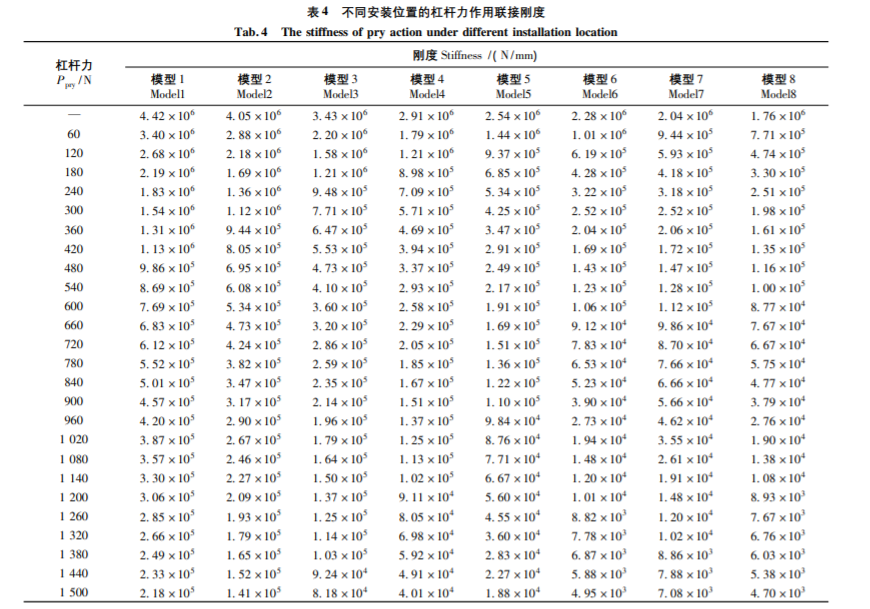
( 1) lb長度越小,，整個聯(lián)接結(jié)構(gòu)的初始剛度就越大，lb增加了30% ,，剛度降低60% ,。

( 2) 隨著lb長度增加，剛度降低的程度逐漸增加,。綜合上述分析,，該參數(shù)對聯(lián)接結(jié)構(gòu)剛度的影響較大，在設(shè)計螺栓聯(lián)接結(jié)構(gòu)時,，保證實(shí)際安裝尺寸的前提 下,，應(yīng)盡量將lb縮短,。

3 剛度擬合公式

綜合上述分析可以看出，聯(lián)接剛度隨著杠桿力的作用發(fā)生了很大的變化,，聯(lián)接剛度是結(jié)構(gòu)進(jìn)行動力學(xué)分析的最重要條件,，因此合理的預(yù)測和分析該參數(shù)對于動力計算有至關(guān)重要的影響。對預(yù)緊力和杠桿力作用距離lb對結(jié)構(gòu)剛度的影響進(jìn)行了分析,，隨著杠桿力的增加,，聯(lián)接結(jié)構(gòu)剛度顯著下降。分析其下降趨勢符合雙指數(shù)形式的類型,，考慮選取參數(shù)進(jìn)行擬合,，擬合公 式( 5) ，分別選取預(yù)緊力及杠桿力影響因子為自變量參數(shù),，根據(jù)表2 和表4的數(shù)據(jù)對其余參數(shù)進(jìn)行擬合[10],。

3. 1 Ppre剛度擬合公式

表3列出了6種預(yù)緊力條件下杠桿力作用的剛度計算結(jié)果，分別對上述參數(shù)采用式(5)進(jìn)行擬合,，得到不同預(yù)緊力作用下的剛度計算結(jié)果與擬合結(jié)果對比如圖9所示,，各參數(shù)隨著預(yù)緊力的不同而變化，選用線性擬合參數(shù),，計算結(jié)果如式：

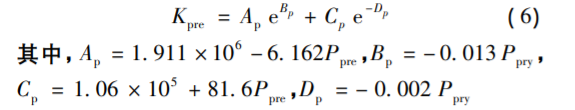
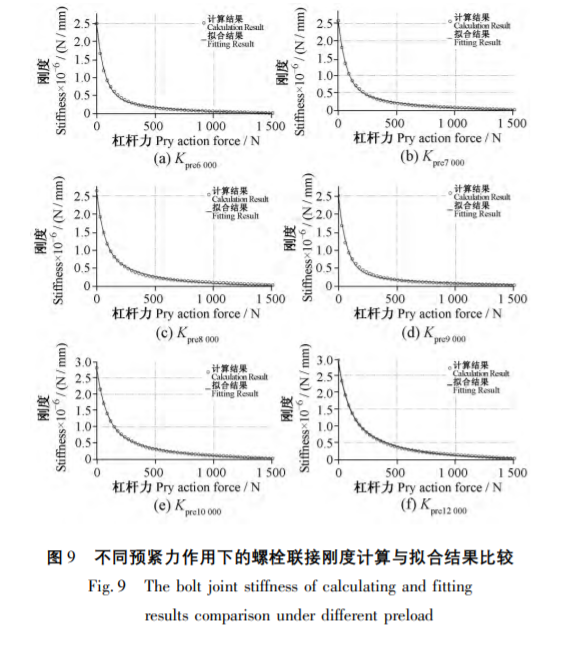
從擬合結(jié)果和數(shù)值計算結(jié)果中可以看出,，兩者可以很好的吻合。

3. 2 fpry剛度擬合公式

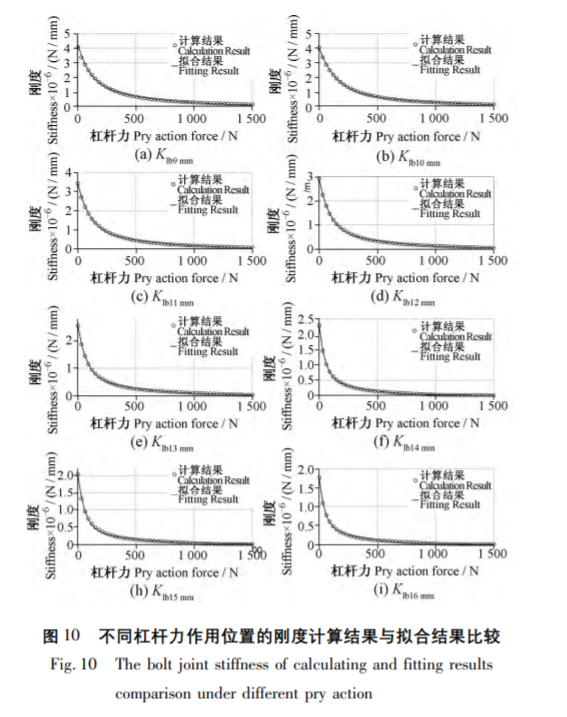
在影響因素中,，lb的影響較大,，對于該參數(shù)，表5列出了8個不同杠桿力作用距離的剛度計算結(jié)果,，由于參數(shù)C的計算結(jié)果離散度較大,，采用二次擬合，得到如式( 7) ,，計算結(jié)果與擬合結(jié)果對比如圖10所示,。同樣采用上述計算方法進(jìn)行擬合計算：

選擇合理的方式對計算數(shù)據(jù)進(jìn)行擬合可以得到杠桿力與聯(lián)接剛度之間的計算公式，該方法可以提供工程計算中不同預(yù)緊力作用下剛度變化以及不同安裝位置的簡化分析,，對于實(shí)際應(yīng)用中進(jìn)行動力學(xué)變剛度分析,，提供了基礎(chǔ)剛度的研究依據(jù)有著很重要的意義。

4 結(jié)論

本文對螺栓聯(lián)接初始剛度及在杠桿力作用下的剛度變化及其影響因素進(jìn)行了分析,，得到了以下幾點(diǎn)結(jié)論:

(1) 計算了杠桿力作用下螺栓聯(lián)接整體剛度隨著杠桿力增加而不斷減少的規(guī)律,，該結(jié)果與文獻(xiàn)[3]的計算結(jié)果吻合。

(2) 分析了不同預(yù)緊力作用下螺栓聯(lián)接承受杠桿力的整體剛度變化規(guī)律,，得到預(yù)緊力作為聯(lián)接的很重要因素,，較大的預(yù)緊力可以保證結(jié)構(gòu)的初始剛度，但是影響較為有限,，預(yù)緊力增加 100% 的條件下,，初始剛度增加13% ,。并且在杠桿力作用過程中，其不同預(yù)緊力其結(jié)構(gòu)整體剛度減小的幅度基本相同,，所以對于該類型受力結(jié)構(gòu)要保證結(jié)構(gòu)整體剛度,，預(yù)緊力并不是最重 要的因素。

( 3) 分析了杠桿力作用線距離螺栓中心的距離對承受杠桿力作用的整體剛度變化規(guī)律,，距離越短,，整個聯(lián)接結(jié)構(gòu)的初始剛度就越大，該距離增加30%,，剛度降低60%,。同時在杠桿力作用過程中，距離越短,，整體剛度減小幅度越小,，距離是影響結(jié)構(gòu)剛度的首要因 素。

( 4) 分別對不同預(yù)緊力及不同距離的螺栓聯(lián)接剛度變化進(jìn)行了公式擬合,，為動力學(xué)分析提供了基礎(chǔ)剛度的研究依據(jù),。